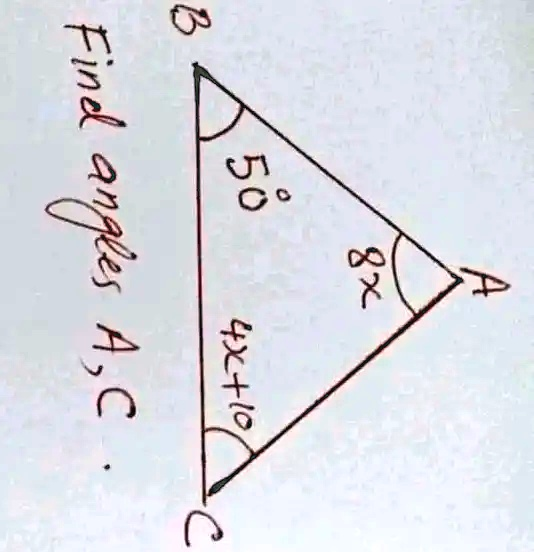
Find angles A, C. B 50° 4x+10 C 8x A
The Correct Answer and Explanation is:
Correct Answer:
Angle A = 80°
Angle C = 50°
Explanation:
To find the measures of angles A and C, we must use the fundamental geometric principle that the sum of the interior angles of any triangle is always 180 degrees. The problem provides the measures of the three angles in a triangle labeled A, B, and C. Angle B is given as a constant value, while angles A and C are given as algebraic expressions involving a variable, x.
The given angles are:
- Angle A = 8x
- Angle B = 50°
- Angle C = 4x + 10
According to the angle sum theorem for triangles:
Angle A + Angle B + Angle C = 180°
We can substitute the given expressions and value into this equation to solve for x:
(8x) + (50) + (4x + 10) = 180
First, we simplify the equation by combining like terms. We add the terms with the variable x together (8x + 4x) and the constant numbers together (50 + 10):
12x + 60 = 180
Next, to isolate the term with x, we subtract 60 from both sides of the equation:
12x = 180 – 60
12x = 120
Now, we solve for x by dividing both sides of the equation by 12:
x = 120 / 12
x = 10
With the value of x determined, we can now find the specific degree measures for Angle A and Angle C by substituting x = 10 back into their original expressions.
For Angle A:
Angle A = 8x
Angle A = 8 * (10)
Angle A = 80°
For Angle C:
Angle C = 4x + 10
Angle C = 4 * (10) + 10
Angle C = 40 + 10
Angle C = 50°
To verify our solution, we can add the three angles to ensure they sum to 180°:
Angle A + Angle B + Angle C = 80° + 50° + 50° = 180°.
The sum is correct, confirming our calculated values for angles A and C.
