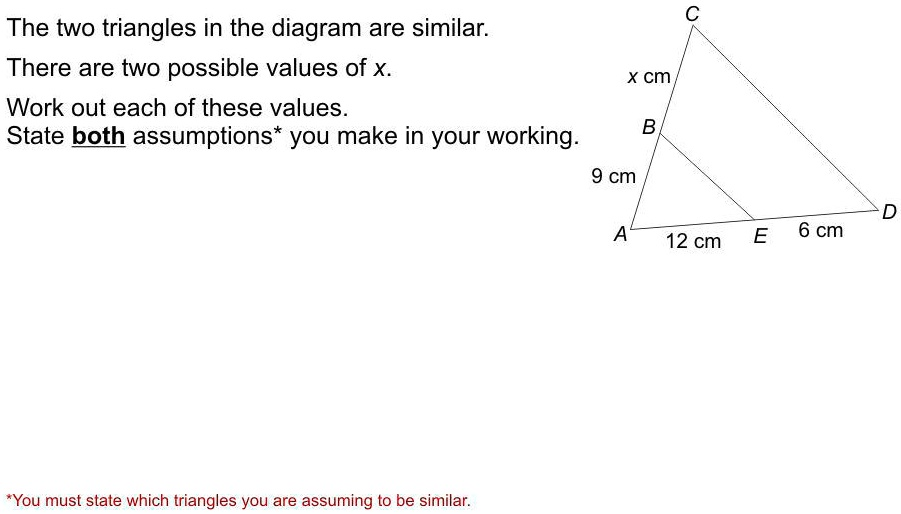
The two triangles in the diagram are similar. There are two possible values of x. Work out each of these values. State both assumptions you make in your working. *You must state which triangles you are assuming to be similar. C x cm B 9 cm D A 12 cm E 6 cm
The Correct Answer and Explanation is:
Here are the two possible values for x, along with the required assumptions and working.
The two triangles in the diagram are the smaller triangle ABE and the larger triangle ACD. The problem states they are similar, but there are two ways this similarity can occur, leading to two different values for x.
First Possible Value
Assumption 1: Triangle ABE is similar to triangle ACD.
This assumption means the triangles are oriented in the same way, with corresponding vertices being A→A, B→C, and E→D. This implies that angle ABE equals angle ACD and angle AEB equals angle ADC.
For these similar triangles, the ratio of their corresponding sides must be equal. We can write the proportion:
AB / AC = AE / AD
We are given the following lengths:
- AB = 9 cm
- AE = 12 cm
- BC = x cm, so AC = AB + BC = 9 + x cm
- ED = 6 cm, so AD = AE + ED = 12 + 6 = 18 cm
Substitute these values into the proportion:
9 / (9 + x) = 12 / 18
To solve for x, first simplify the fraction on the right: 12 / 18 = 2 / 3.
9 / (9 + x) = 2 / 3
Now, cross-multiply:
3 * 9 = 2 * (9 + x)
27 = 18 + 2x
2x = 27 – 18
2x = 9
x = 4.5
Second Possible Value
Assumption 2: Triangle ABE is similar to triangle ADC.
This assumption means the correspondence of vertices is A→A, B→D, and E→C. Here, the angles correspond differently: angle ABE equals angle ADC and angle AEB equals angle ACD.
The ratio of corresponding sides for this similarity is:
AB / AD = AE / AC
Using the same side lengths:
- AB = 9 cm
- AD = 18 cm
- AE = 12 cm
- AC = 9 + x cm
Substitute these values into the proportion:
9 / 18 = 12 / (9 + x)
Simplify the fraction on the left: 9 / 18 = 1 / 2.
1 / 2 = 12 / (9 + x)
Now, cross-multiply:
1 * (9 + x) = 2 * 12
9 + x = 24
x = 24 – 9
x = 15
Therefore, the two possible values of x are 4.5 and 15.
