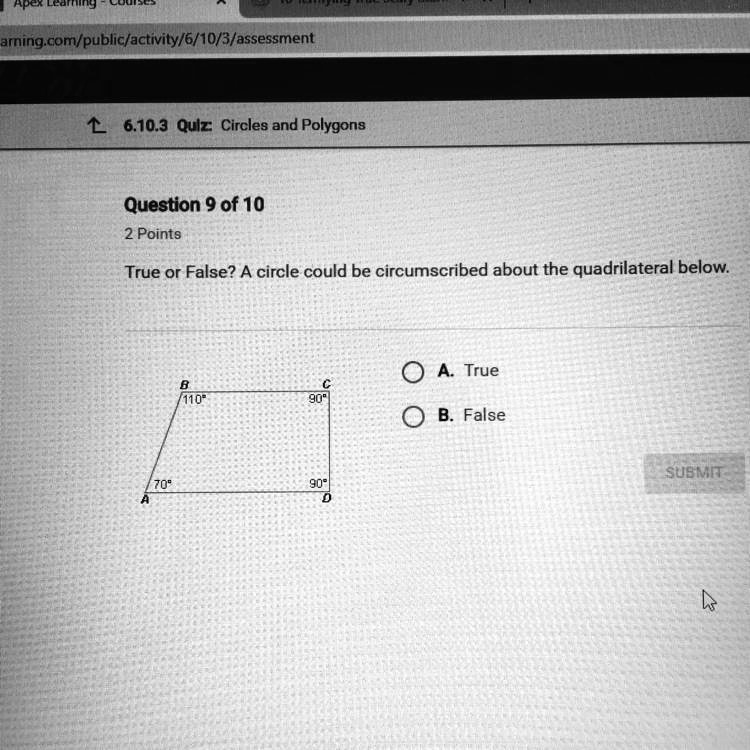
Apex Learning arning.com/public/activity/6/10/3/assessment ?6.10.3 Quiz: Circles and Polygons Question 9 of 10 2 Points True or False? A circle could be circumscribed about the quadrilateral below. A. True B C 110° 90° B. False 70° A 90° D SUBMIT
The Correct Answer and Explanation is:
The correct answer is B. False.
A circle can be circumscribed about a quadrilateral if and only if the quadrilateral is a cyclic quadrilateral. A key property of a cyclic quadrilateral is that its opposite angles are supplementary, meaning that the sum of each pair of opposite angles is exactly 180 degrees. If this condition is not met, a circle cannot be drawn to pass through all four vertices of the quadrilateral.
To determine if the given quadrilateral can have a circumscribed circle, we must check if its opposite angles are supplementary. The quadrilateral shown has vertices A, B, C, and D with the following interior angles:
- Angle A = 70°
- Angle B = 110°
- Angle C = 90°
- Angle D = 90°
First, we check the sum of the first pair of opposite angles, Angle A and Angle C:
Sum = Angle A + Angle C
Sum = 70° + 90° = 160°
The sum of this pair of opposite angles is 160 degrees, which is not equal to 180 degrees. Since this condition fails, we can already conclude that the quadrilateral is not cyclic.
For completeness, we can also check the other pair of opposite angles, Angle B and Angle D:
Sum = Angle B + Angle D
Sum = 110° + 90° = 200°
The sum of this second pair is 200 degrees, which also is not equal to 180 degrees.
Because neither pair of opposite angles is supplementary, the quadrilateral does not satisfy the necessary condition for being a cyclic quadrilateral. Therefore, a circle cannot be circumscribed about it. The statement is false.
