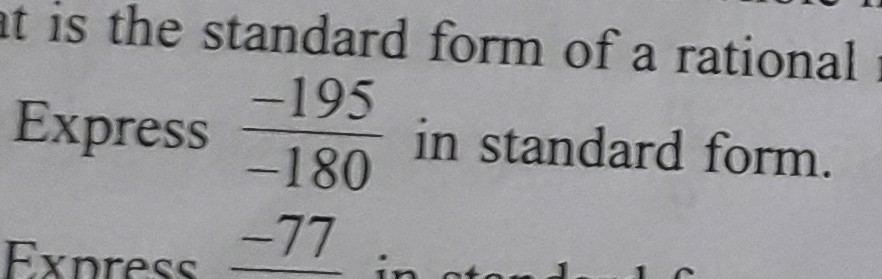
The Correct Answer and Explanation is:
The standard form of the rational number -195/-180 is 13/12.
Explanation
To express a rational number in its standard form, two conditions must be met. First, the denominator of the fraction must be a positive integer. Second, the numerator and the denominator must be coprime, meaning their greatest common divisor (GCD) is 1. This is equivalent to saying the fraction must be reduced to its simplest form. Let’s apply this process to the fraction -195/-180.
Step 1: Make the Denominator Positive
The given fraction is -195/-180. The denominator, -180, is negative. The first rule of standard form requires a positive denominator. We can achieve this by multiplying both the numerator and the denominator by -1. This action does not alter the value of the fraction.
(-195 × -1) / (-180 × -1) = 195/180
A simpler way to think about this is that dividing a negative number by another negative number results in a positive number. Therefore, the two negative signs cancel each other out, leaving us with the equivalent positive fraction 195/180.
Step 2: Simplify the Fraction to its Lowest Terms
Now we have the fraction 195/180. The second condition for standard form is that the numerator and denominator must be coprime. To satisfy this, we must simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor.
We can find the GCD by identifying common factors. We can see that both 195 and 180 are divisible by 5, because their last digits are 5 and 0, respectively.
- 195 ÷ 5 = 39
- 180 ÷ 5 = 36
Dividing both parts of the fraction by 5 gives us 39/36. Now we must check if 39 and 36 have any common factors. Both numbers are divisible by 3.
- 39 ÷ 3 = 13
- 36 ÷ 3 = 12
This simplifies the fraction further to 13/12. The greatest common divisor of the original numbers, 195 and 180, is the product of the factors we divided by, which is 5 × 3 = 15.
The final fraction is 13/12. We check if it is in standard form. The denominator, 12, is positive. The numerator is 13, which is a prime number. Since 12 is not a multiple of 13, the only common factor between 13 and 12 is 1. Thus, they are coprime. Both conditions for standard form are now met.
