The Correct Answer and Explanation is:
The value of cos C is 0.80.
To find the value of the cosine of an angle in a right-angled triangle, we use the trigonometric ratio known as SOH CAH TOA. The “CAH” part of this mnemonic represents the formula for cosine: Cosine = Adjacent / Hypotenuse. This means the cosine of an angle is the ratio of the length of the side adjacent (next to) the angle to the length of the hypotenuse.
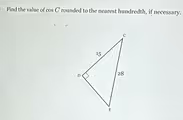
In the provided triangle, the right angle is at vertex B. For angle C, the adjacent side is BC, and the hypotenuse, which is the side opposite the right angle, is CF.
It is important to note that the diagram contains a geometric impossibility. It labels the adjacent side BC as 35 and the hypotenuse CF as 28. In any right-angled triangle, the hypotenuse must be the longest side, but here it is shown as being shorter than one of the legs (28 < 35).
Assuming this is a common type of error in textbook diagrams where the numbers have been accidentally swapped, we will proceed with the logically correct dimensions. We will assume the adjacent side (BC) is 28 and the hypotenuse (CF) is 35. This creates a valid triangle where the hypotenuse is the longest side.
Using these corrected values, we can apply the cosine formula:
cos C = Adjacent / Hypotenuse
cos C = 28 / 35
To simplify this fraction, we can divide both the numerator and the denominator by their greatest common divisor, which is 7.
cos C = 28 ÷ 7 / 35 ÷ 7 = 4 / 5
To express this as a decimal, we perform the division:
cos C = 4 ÷ 5 = 0.8
The question asks for the answer to be rounded to the nearest hundredth. To write 0.8 to the hundredths place, we add a trailing zero, which gives us 0.80.
