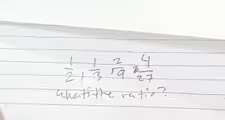
The Correct Answer and Explanation is:
Of course. Here is the answer and a detailed explanation.
The correct ratio is 2/3.
This sequence of numbers, 1/2, 1/3, 2/9, 4/27, is a geometric sequence. A geometric sequence is a series of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. The question asks us to identify this specific number.
To find the common ratio, you can divide any term in the sequence by the term that comes immediately before it. We can perform this calculation for each pair of consecutive terms to confirm that the ratio is constant.
Let’s start with the first two terms:
(Second Term) / (First Term) = (1/3) / (1/2)
To divide by a fraction, you multiply by its reciprocal. The reciprocal of 1/2 is 2/1.
So, the calculation is (1/3) * (2/1) = 2/3.
Now, let’s verify this using the next pair of terms, the third and the second:
(Third Term) / (Second Term) = (2/9) / (1/3)
Again, we multiply by the reciprocal of the second fraction. The reciprocal of 1/3 is 3/1.
So, the calculation is (2/9) * (3/1) = 6/9.
The fraction 6/9 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 3. This gives us 2/3.
Finally, we can check the last pair of terms to be certain:
(Fourth Term) / (Third Term) = (4/27) / (2/9)
Multiplying by the reciprocal of 2/9 gives us:
(4/27) * (9/2) = 36/54.
This fraction can also be simplified. Both 36 and 54 are divisible by 18, which gives us 2/3.
Since the result is consistently 2/3 for every pair of consecutive terms, we can confidently state that the common ratio for this geometric sequence is 2/3.
