The Correct Answer and Explanation is:
Correct Answer: The first three terms of the sequence are a_1, a_1 * r, and a_1 * r^2.
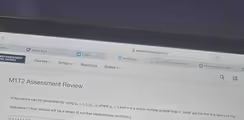
The image displays a mathematical problem concerning a recursive sequence from an “M1T2 Assessment Review”. The problem provides a recursive formula, a_n = a_(n-1) * r, which is the standard definition for a geometric sequence. This formula states that any term in the sequence (a_n) is found by multiplying the term that comes immediately before it (a_(n-1)) by a constant value r, known as the common ratio. The problem also specifies a condition for the first term, a_1, which must be a whole number greater than 1. However, it does not provide specific numerical values for either the first term a_1 or the common ratio r.
Because these specific values are not given, it is impossible to provide a numerical answer. The correct approach is to express the first three terms of the sequence algebraically, using the variables a_1 and r.
The first term is, by definition, a_1.
To find the second term, a_2, we use the recursive formula with n=2. The formula becomes a_2 = a_(2-1) * r, which simplifies to a_2 = a_1 * r. This means the second term is the first term multiplied by the common ratio.
To find the third term, a_3, we again use the formula, this time with n=3. This gives us a_3 = a_(3-1) * r, which simplifies to a_3 = a_2 * r. Since we already determined that a_2 is equal to a_1 * r, we can substitute this expression into the equation for a_3. This results in a_3 = (a_1 * r) * r, which simplifies to a_3 = a_1 * r^2.
Therefore, the general forms for the first three terms of this geometric sequence are a_1, a_1 * r, and a_1 * r^2. For any chosen whole number a_1 greater than 1 and any common ratio r, these expressions will yield the correct terms.
