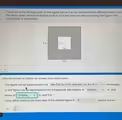
The Correct Answer and Explanation is:
Of course. Based on the image provided, here is the correct answer and a detailed explanation.
Correct Answer: The single expression for the area of the shaded region is a² – b², which can also be factored as (a – b)(a + b).
Explanation
The problem asks for a single expression representing the area of the shaded gray region. This region is a large square with a smaller square removed from its center. To find this area, we use a straightforward geometric principle: calculate the area of the larger shape and subtract the area of the smaller shape that has been cut out.
First, we must identify the areas of the two individual squares. The formula for the area of any square is its side length multiplied by itself, or side². Let’s assign variables to the side lengths shown in the diagram. We will let a represent the side length of the large gray square (labeled Side A) and b represent the side length of the smaller white square (labeled Side B).
Using the area formula:
- The total area of the large square is a × a = a².
- The area of the small white square that is removed is b × b = b².
Next, to find the area of only the shaded portion, we subtract the area of the white square from the area of the large square. This gives us the expression:
Area of Shaded Region = (Area of Large Square) – (Area of Small Square)
Area of Shaded Region = a² – b²
This expression, a² – b², is the most direct answer. It is also a notable algebraic identity known as the “difference of squares.” This identity can be factored into the product of two terms: (a – b)(a + b). Both a² – b² and (a – b)(a + b) are correct expressions for the shaded area, with the latter being the factored form.
