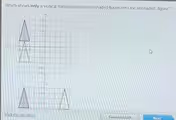
The Correct Answer and Explanation is:
The correct choice is the figure located on the right. This answer is correct because it is the only option that accurately represents a vertical translation of the original figure.
A vertical translation is a geometric transformation that moves every point of a figure up or down by the same distance. When a figure undergoes a vertical translation on a coordinate plane, its orientation and size remain the same. Critically, the x-coordinates of all its points do not change, while the y-coordinates are all increased or decreased by a constant value.
The original figure, positioned at the top of the image, is located in the first quadrant, with its x-coordinates ranging from 1 to 3. To identify the correct vertical translation, we must find the option where the figure has been moved only vertically.
The figure on the left has been moved to the third quadrant. Its x-coordinates are now negative, which means it has undergone a horizontal shift in addition to a vertical one. Therefore, it is not a pure vertical translation.
The figure on the right, however, is a perfect example of a vertical translation. Its x-coordinates remain between 1 and 3, identical to the original figure. Every point has been shifted straight down by 5 units. For instance, the topmost point of the original figure at coordinate (2, 5) has moved to (2, 0). This consistent downward shift, without any horizontal change, fulfills the definition of a vertical translation.
It is important to note that the question contains a factual error. It asks for a translation into the second quadrant, which has negative x-coordinates. A vertical translation cannot move a figure from the first quadrant (positive x-values) to the second quadrant. The translated figure on the right is actually in the fourth quadrant. Despite this error in the prompt, the figure on the right is the only one that depicts a vertical translation, making it the intended answer.
