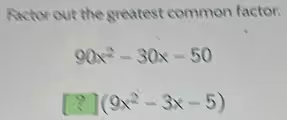
The Correct Answer and Explanation is:
The correct answer is 10.
To solve this problem, we need to find the greatest common factor (GCF) of the polynomial 90x² – 30x – 50. The greatest common factor is the largest factor that divides all the terms of the polynomial without leaving a remainder. The process involves examining both the numerical coefficients and the variables of each term.
First, let’s identify the terms in the expression: 90x², -30x, and -50.
Next, we find the GCF of the numerical coefficients: 90, 30, and 50. To do this, we can list the factors of each number to find the largest one they all share.
- Factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30.
- Factors of 50 are 1, 2, 5, 10, 25, 50.
- Factors of 90 are 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90.
By comparing these lists, we can see that the greatest factor common to all three numbers is 10.
Then, we look at the variable part of each term. The terms have x², x, and no x variable (or x⁰), respectively. Since the last term, -50, does not contain the variable x, we cannot factor out any x from the entire polynomial. Therefore, the variable part of the GCF is 1.
Combining these findings, the greatest common factor for the entire expression 90x² – 30x – 50 is 10.
The final step is to factor out the GCF. This is done by dividing each term in the original polynomial by the GCF (10) and placing the result in parentheses, with the GCF written outside.
- 90x² / 10 = 9x²
- -30x / 10 = -3x
- -50 / 10 = -5
So, the factored form of the expression is 10(9x² – 3x – 5). The number that belongs in the box with the question mark is 10.
