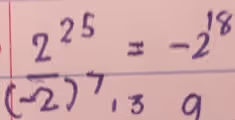
The Correct Answer and Explanation is:
The correct answer to the expression is -2^(43/2).
The problem requires simplifying the expression 2^25 / (-√2)^7. To solve this, we can break it down into a few key steps, focusing on simplifying the denominator first and then applying the rules of exponents.
First, let’s address the denominator, which is (-√2)^7. When a negative number is raised to an odd power, the result is negative. Therefore, (-√2)^7 is equal to -(√2)^7. This isolates the negative sign, which we will carry through the calculation.
Next, we simplify (√2)^7. The square root of 2, or √2, can be written in exponential form as 2^(1/2). So, (√2)^7 is the same as (2^(1/2))^7. Using the power of a power rule for exponents, which states that (a^m)^n = a^(m*n), we multiply the exponents. This gives us 2^((1/2) * 7), which simplifies to 2^(7/2). Combining this with the negative sign from earlier, the entire denominator, (-√2)^7, simplifies to -2^(7/2).
Now, we can substitute this simplified denominator back into the original expression. The problem becomes 2^25 / (-2^(7/2)).
Finally, we perform the division. A positive number divided by a negative number results in a negative answer. We apply the quotient rule for exponents, which states that a^m / a^n = a^(m-n). In our case, this means we subtract the exponent in the denominator from the exponent in the numerator: 25 – 7/2. To perform this subtraction, we find a common denominator, converting 25 to 50/2. The calculation is 50/2 – 7/2 = 43/2.
Combining the negative sign and the new exponent, the final simplified answer is -2^(43/2).
