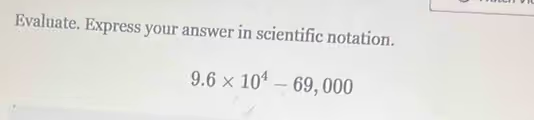
The Correct Answer and Explanation is:
Correct Answer: 2.7 × 10⁴
Explanation
The problem requires us to evaluate the expression 9.6 × 10⁴ – 69,000 and express the result in scientific notation. To perform an operation like subtraction, both numbers must be in the same format. We can achieve this by converting both numbers to standard decimal form or by ensuring both are in scientific notation with the same power of ten. Let’s use the second method, as it is often more direct when the final answer must be in scientific notation.
Step 1: Convert both numbers to the same format.
The first number, 9.6 × 10⁴, is already in scientific notation. We need to convert the second number, 69,000, into scientific notation. Scientific notation represents a number as a coefficient (a number between 1 and 10) multiplied by a power of 10.
For the number 69,000, the decimal point is implicitly at the end (69,000.). To get a coefficient between 1 and 10, we need to move the decimal point to the left until it sits after the first non-zero digit, which is 6. This gives us 6.9. We moved the decimal point four places to the left, so the exponent of 10 will be 4.
Therefore, 69,000 = 6.9 × 10⁴.
Step 2: Perform the subtraction.
Now we can rewrite the original expression with both terms in the same scientific format:
9.6 × 10⁴ – 6.9 × 10⁴
Since both terms have the same power of ten (10⁴), we can subtract the coefficients directly. This is similar to combining like terms in algebra. We can factor out the common power of ten:
(9.6 – 6.9) × 10⁴
Now, we subtract the coefficients:
9.6 – 6.9 = 2.7
Step 3: Write the final answer in scientific notation.
We combine the new coefficient with the power of ten to get the final result:
2.7 × 10⁴
This answer is already in proper scientific notation because the coefficient, 2.7, is a number between 1 and 10.
To verify our work, we can also solve this by converting both numbers to standard form first.
9.6 × 10⁴ = 96,000
96,000 – 69,000 = 27,000
Converting 27,000 back to scientific notation gives 2.7 × 10⁴, which confirms our answer.
