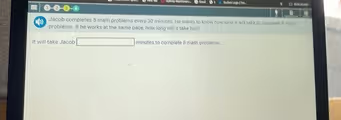
The Correct Answer and Explanation is:
The correct answer is 32.
Here is a detailed explanation of how to arrive at this solution.
The problem requires us to determine the total time it will take for Jacob to complete 8 math problems, based on his established working speed. The information provided is that he completes 5 math problems in 20 minutes. The key assumption is that he maintains this same pace for all the problems. There are two primary methods to solve this type of rate problem.
Method 1: Finding the Unit Rate
The first and often most intuitive method is to calculate the unit rate. In this context, the unit rate is the amount of time it takes Jacob to complete one single math problem. To find this, we can divide the total time he spent by the number of problems he completed in that time.
The given rate is 5 problems per 20 minutes.
Calculation for time per problem:
Total Time / Number of Problems = Time per Problem
20 minutes / 5 problems = 4 minutes per problem
This calculation tells us that Jacob spends exactly 4 minutes on each math problem he solves. Now that we have this unit rate, we can easily find out how long it would take him to complete any number of problems. The question asks for the time it will take to complete 8 problems. We can find this by multiplying the number of problems by the time it takes to complete one problem.
Calculation for 8 problems:
Number of Problems × Time per Problem = Total Time
8 problems × 4 minutes/problem = 32 minutes
Therefore, it will take Jacob 32 minutes to complete 8 math problems.
Method 2: Using Proportions
A second reliable method for solving this problem is to set up a proportion. A proportion is an equation that states two ratios or fractions are equal. We can set up a ratio of problems to minutes.
Our known ratio is 5 problems to 20 minutes. We can write this as the fraction 5/20.
Our unknown ratio involves 8 problems and an unknown number of minutes, which we can call ‘x’. We can write this as the fraction 8/x.
Since Jacob works at the same pace, these two ratios must be equivalent. We can set them equal to each other to form a proportion:
5 / 20 = 8 / x
To solve for ‘x’, we use a technique called cross multiplication. We multiply the numerator of the first fraction by the denominator of the second, and set that equal to the product of the denominator of the first fraction and the numerator of the second.
5 * x = 20 * 8
5x = 160
Now, to find the value of x, we need to isolate it by dividing both sides of the equation by 5:
x = 160 / 5
x = 32
Both methods yield the same result, confirming that it will take Jacob 32 minutes to complete 8 math problems.
