The Correct Answer and Explanation is:
The correct answer is x = 4.5.
Explanation:
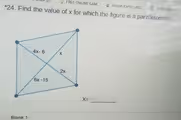
The problem asks to find the value of x that makes the given quadrilateral a parallelogram. A key property of all parallelograms is that their diagonals bisect each other. This means that the point where the two diagonals intersect cuts each diagonal into two segments of equal length.
In the provided figure, we have two diagonals.
The first diagonal is divided into segments with lengths represented by the expressions 4x – 6 and 6x – 15. For the figure to be a parallelogram, these two segments must be equal to each other. This gives us our first equation:
4x – 6 = 6x – 15
The second diagonal is divided into segments with lengths x and 2x. For the figure to be a parallelogram, these segments must also be equal. This would give us a second equation:
x = 2x
If we analyze the second equation, subtracting x from both sides gives 0 = x. However, if x were 0, the first diagonal’s segments would have lengths of 4(0) – 6 = -6, which is impossible, as a geometric length cannot be negative. This indicates there is a contradiction or error in the labeling of the second diagonal in the problem diagram.
Therefore, we proceed by solving the first equation, which is derived from the other diagonal and will yield a valid geometric solution.
To solve for x, we set the expressions for the segments of the first diagonal equal to each other:
4x – 6 = 6x – 15
First, we can gather the x terms on one side of the equation by subtracting 4x from both sides:
-6 = 2x – 15
Next, we isolate the term with x by adding 15 to both sides of the equation:
9 = 2x
Finally, we solve for x by dividing both sides by 2:
x = 9 / 2
x = 4.5
When x equals 4.5, the segments of the first diagonal are both 12, confirming they are equal and satisfying the property of a parallelogram.
