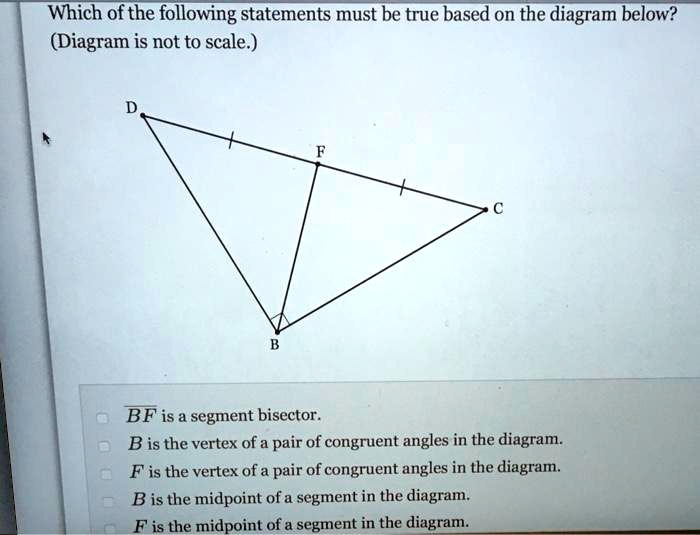
Which of the following statements must be true based on the diagram below? (Diagram is not to scale ) BF is a segment bisector. Bis the vertex of a pair of congruent angles in the diagram Fis the vertex of a pair of congruent angles in the diagram Bis the midpoint ofa segment in the diagram: F is the midpoint of a segment in the diagram
The Correct Answer and Explanation is:
The correct answer is: F is the midpoint of a segment in the diagram.
Explanation:
From the diagram, we observe triangle DBCDBCDBC with a point FFF on segment DCDCDC, and segment BFBFBF connecting point BBB to point FFF. The key visual clues are the tick marks on segments DFDFDF and FCFCFC, which indicate that:DF≅FCDF \cong FCDF≅FC
This tells us that point FFF divides segment DCDCDC into two congruent parts, meaning:F is the midpoint of DC‾.F \text{ is the midpoint of } \overline{DC}.F is the midpoint of DC.
So the only statement that must be true based on the diagram is:
✅ F is the midpoint of a segment in the diagram.
Why the Other Choices Are Incorrect:
- BF is a segment bisector.
- There is no information showing that BFBFBF bisects any other segment. No angles or segments are marked to indicate that BFBFBF cuts another segment into equal parts.
- B is the vertex of a pair of congruent angles in the diagram.
- There are no angle congruence markings at vertex BBB. We cannot assume angle congruence just by visual estimation.
- F is the vertex of a pair of congruent angles in the diagram.
- Again, no angle congruence is indicated at point FFF, only segment congruence.
- B is the midpoint of a segment in the diagram.
- There is no indication that point BBB divides any segment into two equal parts.
Summary:
The only marked congruence is between segments DFDFDF and FCFCFC, which shows that FFF is the midpoint of segment DCDCDC. All other options cannot be confirmed solely from the given diagram. Therefore, the correct and must-be-true statement is:
“F is the midpoint of a segment in the diagram.”
